Theoretical Aspects of Metamaterials and my main fields

Linear Elasticity

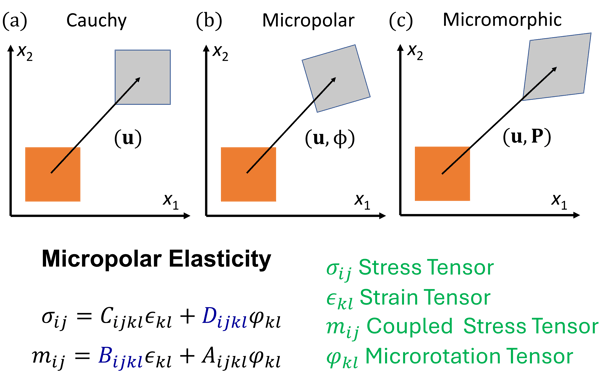
• Cauchy Elasticity (Classical Linear Elasticity)

  • Stress depends only on the symmetric strain tensor

  • The material response is fully described by the Cauchy stress tensor and the elasticity tensor (C).

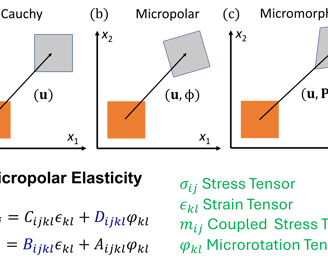
• Micropolar Elasticity (Cosserat Elasticity)

  • Extends Cauchy elasticity by considering couple stresses and microrotations.

  • Each material point has additional degrees of freedom, meaning it can rotate independently of macroscopic deformations.

  • Introduces an additional couple stress tensor and an asymmetric stress tensor.

• Micromorphic Elasticity

  • Generalizes micropolar elasticity by allowing micro-deformations inside each material point, beyond simple rotations.

  • Incorporates an extra micro-distortion tensor that describes how the internal structure deforms.

Transformational Physics

Transformational physics and cloaking are grounded in the fundamental concept of space coordinate transformations, which dictate how physical fields behave under changes in the reference frame. In essence, the governing equations of wave propagation—whether electromagnetic, acoustic, or elastic—can be reformulated in a transformed coordinate system, where the object to be cloaked is effectively "removed" from interaction with incident waves. This relies on the mathematical invariance of fundamental field equations, such as Maxwell’s equations for electromagnetism or the Navier-Cauchy equations for elasticity, under a change of coordinates.

Mathematically, the transformation of coordinates introduces an effective material response governed by the Jacobian tensor J of the transformation, leading to modified constitutive relations. This approach creates an effective material space, where the apparent physics of wave propagation follows the new coordinate frame rather than the Euclidean one, thus achieving cloaking by guiding waves seamlessly around the hidden region.

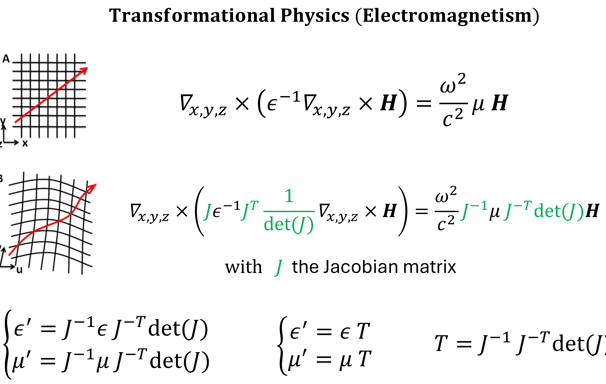
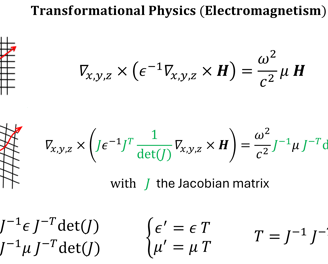
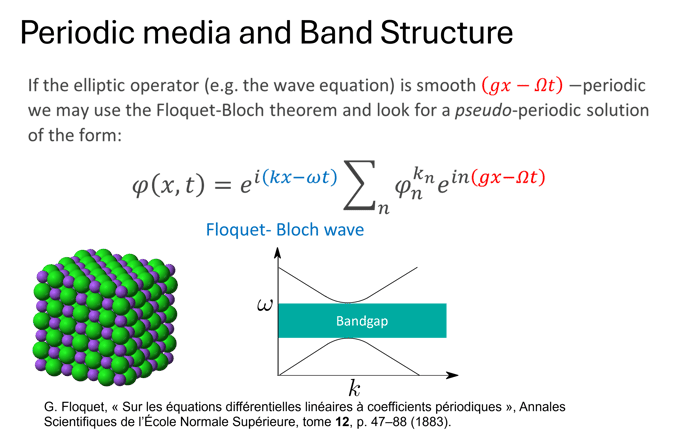
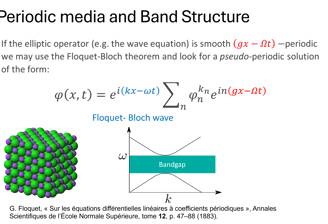
Bloch Modes and Dispersion

Dispersion relations describe how wave frequencies (ω) relate to their wave vectors (k) in a given medium, governing wave propagation characteristics such as phase and group velocities. In phononics, where one studies the propagation of elastic or acoustic waves in periodic structures, dispersion relations are derived from Bloch's theorem, which states that wave solutions in a periodic medium can be expressed as a plane wave modulated by a periodic function.

By solving the eigenvalue problem derived from the elastodynamic equations under periodic boundary conditions, one can ascertain the phononic band structure, represented as discrete branches in omega(k) that correspond to allowed vibrational modes. This formalism uncovers significant wave phenomena, such as bandgaps—specific frequency ranges that inhibit wave propagation due to destructive interference. Additionally, the analysis reveals properties like negative group velocities, contributing to the intricate dynamics present in complex materials. Understanding these elements is crucial for advancements in phononic crystals and related applications in wave manipulation.